Rafsegulfræði 1

Dæmi 2014

1. skammtur fyrir dæmatíma 13. janúar:
1. Mjög langur einangrandi sívalningur með geisla a er með rúmhleðsludreifingu ρ(R)=ρ₀(R/a). Sívalningnum er rennt inn í örþunna kjörleiðandi sívalningsmálmskel með geisla b>a sem er óhlaðin í upphafi þannig að ásar þeirra liggja á sömu línu.
  1. Finnið heildarhleðslu sívalningsins á lengd L.
  2. Finnið rafsviðið innan innri sívalningsins.
  3. Finnið rafsviðið milli og fyrir utan sívalningana.
  4. Hvert er rafmættið á þessum þremur svæðum? Teiknið það upp.
  5. Hvernig er yfirborðshleðslu málskeljarinnar háttað?
2. Getur E(x,y,z)=(0,E₀(x/L),0) verið rafstöðusvið? L er einhver ótiltekin lengd og E₀ er fasti með vídd rafsviðs.
(Skilafrestur: Miðvikudagur 8. janúar 2014 klukkan 17:00),
Lausnir skiladæma

Tímadæmi: 3.18, 3.20, 3.38 og 3.47 í bók

2. skammtur fyrir dæmatíma 20. janúar:
1. Þéttir er gerður úr tveimur sammiðja sívölum kjörleiðurum með geisla a < b og lengd L ≫ b. Þéttirinn er hálffylltur með rafsvarandi vökva með ε_r > 1.
  1. Finnið rýmd þéttisins.
  2. Innri sívalningsskelin er með heildarhleðslu Q. Hve stór hluti hennar er á efri hluta skeljarinnar sem ekki snertir rafsvarann, og hve mikill hluti er á neðri hlutanum í snertingu við rafsvarann?
  3. Er einhver rúmhleðsla dreifð um rafsvarann?
  4. Hver er heildarhleðsla ytri sívalningsins?
  5. Finnið rafstöðuorku kerfisins.
  6. Finnið rafkraftinn sem innri skelin verkar með á þá ytri
(Skilafrestur: Miðvikudagur 15. janúar 2014 klukkan 17:00),
Lausn skiladæmis

Tímadæmi: 4.6, 4.7, 4.10 og 4.12 í bók

3. skammtur fyrir dæmatíma 27. janúar:
1. In the book in Figure 4-15 is shown a system with two grounded semi-infinite parallel conducting plates. At the end of the two plates is a third one perpendicular to them and insulated from the others and held at voltage V₀. We change the third plate to have a linearly varying potential determined by V(y)=V₀(y/b).
  1. Determine the potential V(x,y) between the plates.
  2. Find the surface charge distribution on the end plate.
  3. Find the surface charge distribution on the lower parallel plate.
2. A point charge q is located a distance R_q from the center of a grounded perfectly conducting sphere with radius a. Find the force between the sphere and the charge. R_q > a. Is it attractive or repulsive?

4. skammtur fyrir dæmatíma 3. febrúar:
1. Insulating thin spherical shell with radius a carries a static surface charge ρ_s(θ)= ρ_s0sin(3θ), where ρ_s0 is a constant with the dimension of surface charge density.
  1. Find the electrostatic potential inside and outside the shell
  2. Make a graph of the solution.
  3. What does the asymptotic form of the exterior solution tell us about the charge distribution?
  (Skilafrestur: Miðvikudagur 29. janúar 2014 klukkan 17:00),
  Lausn skiladæmis
  
  Tímadæmi: 5-6, 5-10, 5-13 og 5-21 í bók

5. skammtur fyrir dæmatíma 10. febrúar:
1. A capacitor is made of two ideally conducting concentric metalic spherical shells with radii b>a. It is filled with an imperfect dielectric with permittivity ε(R)=ε₀b/R and conductivity σ(R)=σ₀(R/a)². Both metal hemispheres are very thin. The inner one is connected to the outside with an insulated thin straight perfect conductor that is threaded through a tiny hole in the outer shell. This connector is normal to both shells.
  1. Calculate the conductance of the capacitor
  2. Find the distribution of free charge in the capacitor.
  3. Find the distribution of bound charges of the dielectric.
  4. What is the total free charge in the capacitor?
  5. If we imagine that current I is driven through the system, how is the surface current distribution on the inner shell?
  (Skilafrestur: Miðvikudagur 5. febrúar 2014 klukkan 17:00),
  Lausn skiladæmis
  
  Tímadæmi: 6-4, 6-11, 6-12 og 6-15 í bók

6. skammtur fyrir dæmatíma 17. febrúar:
1. Hollow infinite insulating cylinder with inner radius a and outer radius b is rotated uniformily around its central axis of symmetry with the angular speed ω. The cylinder has a spatial charge distribution ρ(r)=ρ₀(r/a)². Find the magnetic flux density, B everywhere.
2. Two very thin infinite parallel perfectly conducting sheets carry surface current density J_s. The distance between the sheets is d. Find B everywhere for the case of the currents being parallel, and the case when they are antiparallel.

7. skammtur fyrir dæmatíma 24. febrúar:
1. Infinite thick conducting plate of thickness 2d lies parallel to the x-y-plane. The x-y-plane divides the plate, or the slab of material, into two halves. The magnetic susceptibility of the plate is χ_m and it carries a free volume current density J(z)=J₀(z/d)a_x. Determine H, M, and B in all relevant regions.
2. Consider a two-wire line made of two thin parallel wires carrying a DC current in opposite directions. The figure shows two such lines:
  
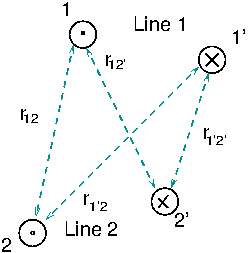
  Find the the mutual inductance of the two two-wire lines per unit length.

8. skammtur fyrir dæmatíma 3. mars:
1. Starting with the two Maxwell's equations containing the curl or rot operator and the continuity equation derive the two Maxwell's equations containing the div operator.
  Do the corresponding for the Maxwell's equations in the integral form. From the two equations containing circulation and the continuity equation derive the two equations containing flux.
2. Metal disk of radius a, thickness d, and conductivity σ lies centered in the x-y-plane. There is a time-dependent uniform magnetic field flux density B(t)=a_zB(t). Determine the induced current density J(r,t) in the disk.

9. skammtur fyrir dæmatíma 10. mars:
1. Gegnsærri rafsvarandi filmu er komið fyrir á glerplötu með ε_r=4.0 og μ_r=1.0 til þess að rautt ljós með λ=700 nm endurkastist ekki af henni. Finnið þykkt filmunnar og ε_r hennar. Sýnið á grafi hvernig ljós með bylgjulengd λ á bilinu 400 nm upp í 750 nm endurkastast af plötunni ef það fellur lóðrétt á hana.
2. Dæmi 8-45 í bók. Túlkið gröfin sem beðið er um.

10. skammtur fyrir dæmatíma 31. mars:
1. Finnið og skoðið TM og TE hættina í loftfylltu sívalnings holi með m,n,p jafna 0 eða 1. Gerum ráð fyrir að d=a. Er eitthvað hægt að segja um skautun þeirra?
2. Í loftneti með lengd L er straumur i(z,t)=Re{I₀sin(2π|z|/L)exp(iωt)}, fyrir |z| ≤ L/2.
  1. Teiknið upp i(z).
  2. Finnið geislunarmynstrið.
  3. Hvaða skaut má greina í geisluninni?

Viðar Guðmundsson
31.03.2014