- Gegnheil rafsvarandi kúla með geisla a er í tómarúmi. Skautun hennar er lýst sem P(R)=P0(R/a)aR. Takið eftir að skautunin er ekki einsleit.
- Finnið bolskautunarhleðsluþéttleika (bulk polarization density) kúlunnar.
- Finnið yfirborðsskautunarhleðsluþéttleika (surface polarization density) kúlunnar.
- Reiknið rafstöðumættið innan og utan kúlunnar.
- Reiknið rafsviðið innan og utan kúlunnar.
- Rissið upp myndir af skautunarhleðslunni (polarization density), mættinu og rafsviðinu sem falli af R.
- Hugsum okkur fyrst einn einangrandi sívalning. Hann er með geisla a og fasta rúmhleðslu +ρ.
Finnið Rafsviðið innan sívalningsins og utan hans.
- Gerið graf af styrk rafsviðins sem falli af fjarlægðinni frá miðjuás sívalningsins. Lýsið og skýrið hegðun sviðsins við yfirborð sívalningsins.
- Nú er öðrum sívalningi með föstu rúmhleðslunni -ρ komið fyrir samsíða hinum fyrri þannig að þeir skarist og fjarlægð ása þeirra sé fastinn d. Finnið rafsviðið þar sem þeir skarast.
(Skilafrestur: Miðvikudagur 14. janúar 2015 klukkan 17:00),
Lausnir skiladæma
Tímadæmi: 3-18, 3-20, 3-38 og 3-47 í bók
- Þéttir er gerður úr tveimur samhliða mjög stórum kjörleiðandi (ideally conducting) plötum. Bilið milli platnanna er d og er fyllt með einangrandi rafsvara (dielectric) með εr(x)=((d+x)/d)2, þar sem x er fjarlægðin mæld frá annarri plötunni til hinnar.
- Finnið rýmd (capacity) þéttisins. Skýrið og réttlætið skrefin sem tekin eru til þess.
- Kannið hvort og þá hvernig skautunarhleðslurnar í og á rafsvaranum eru háðar spennunni sem lögð er yfir þéttinn.
- Hugsum okkur gegnheila óhlaðna kjörleiðandi kúlu með geisla R0.
Innan í henni holum við út kúlulaga holrúm sem snertast ekki,
né heldur yfirborð kúlunnar. Annað holrúmið er með geisla a
og punkthleðslu qa í miðju þess. Hitt er með geisla
b og punkthleðslu qb í miðju þess. Svarið og skýrið:
- Finnið yfirborðshleðslur kúlunnar og kúluholrúmanna innan hennar.
- Hvert er rafsviðið utan kúlunnar?
- Hvert er rafsviðið innan hvers holrúms?
- Hver er krafturinn sem verkar á hvora punkthleðslu?
- Hvað breytist ef enn ein punkthleðslan er sett utan kúlunnar?
(Skilafrestur: Miðvikudagur 21. janúar 2015 klukkan 17:00),
Lausn skiladæma
Tímadæmi: 4-6, 4-7, 4-10 og 4-12 í bók
- Holur teningur er gerður úr kjörleiðandi ferningum með hliðlengd a.
Hliðar teningsins eru einangraðar frá hver annarri. Topphliðinni
og botnhliðinni er haldið við fasta jákvæða spennu V0,
en hinar fjórar hliðarnar eru allar jarðtengdar.
- Finnið rafstöðumættið alls staðar inni í teningnum.
- Finnið yfirborðshleðsluþéttleikann á topphliðinni.
- Gerið graf af yfirborðshleðslunni á topphliðinni.
- Finnið einhverjar leiðir til að sýna mættið á gröfum.
(Skilafrestur: Miðvikudagur 28. janúar 2015 klukkan 17:00),
Lausn skiladæmis, gröf og skriftur
Tímadæmi: 4-17, 4-25, 4-26 og 4-29 í bók
- Löng einangrandi örþunn sívalningsskel með geisla a ber yfirborðshleðsluþéttleikann
ρs(φ)=ρs0 sin(3φ).
- Finnið rafstöðumættið og rafsviðið innan og utan hennar.
- Gerið graf af rafstöðumættinu.
- Hvernig tengjast heildarhleðsla sívalningsins og aðfellulausn (asymptotic solution) rafmættisins fjarri honum?
(Skilafrestur: Miðvikudagur 4. febrúar 2015 klukkan 17:00),
Lausn skiladæmis, gröf og skriftur.
Tímadæmi: 5-6, 5-10, 5-13 og 5-21 í bók
- Í stórum einsleitum efnisbúti með eðlisleiðni σ flýtur
straumur með þéttleika J
=azJ0.
- Finnið straumþéttleikann ef kúluholrúmi með geisla a er komið fyrir inni í efnisbútnum.
- Berið straumsviðið saman við rafsviðið í kringum kjörleiðandi kúlu í föstu ytra rafsviði. Hvað er ólíkt?
- Gerið graf af straumþéttleikanum í kringum kúluna
- Hér er sýnidæmi um vigursviðsmynd með gnuplot.
(Skilafrestur: Miðvikudagur 11. febrúar 2015 klukkan 17:00),
Lausn skiladæmis, gröf og skriftur.
Tímadæmi: 6-4, 6-11, 6-12 og 6-15 í bók
- Langur sívalningur með geisla a ber seglun M =M0(r/a)2aφ. Finnið segulflæðisviðið (magnetic flux density) innan og utan sívalningsins.
- Þvert á langás sívalnings með geisla a og segulsvörunarstuðul μ
liggur fast segulflæðisvið.
- Finnið B, H og M innan og utan sívalningsins.
- Rissið upp myndir af B fyrir sívalning sem er sterklega andseglandi (diamagnetic), eða sterklega meðseglandi (paramagnetic).
(Skilafrestur: Miðvikudagur 18. febrúar 2015 klukkan 17:00),
Lausnir skiladæma
Tímadæmi: 6-34, 6-35, 6-39 og 6-53 í bók
- Skoðum aðeins hvernig lögmál Faradays breytir hugmyndum um
spennu og spennumælingu. Á myndinni eru tveir eins spennumælar
með mjög hátt innra viðnám R >> Ra, Rb settir saman í einfalda rás til
þess að mæla spennu yfir tvö viðnám Ra og Rb.
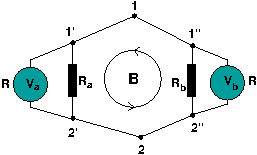
Segulflæðið í spólunni vex sem Φ(t)=αt. Reiknið strauminn um rásina ef gert er ráð fyrir því að enginn straumur fari um spennumælana. Hvaða spennu sýnir hvor mælir? Hvað er einkennilegt við niðurstöðurnar þegar þær eru bornar saman við reynsluna af jafnstraumsrásum? Fjölmargir hafa skrifað greinar um þetta dæmi og W. Lewin þurfti að gera tilraunina í tíma til að sannfæra meðkennara og nemendur um niðurstöðuna. - Segulflæði um hringlaga lykkju með geisla a, sjálfspan L0 og viðnám R0 er Φ(t)=Φ0erf(αt). Finnið strauminn i(t) um lykkjuna og ákvarðið hve mikil heildarhleðsla hefur flust um sérhvern punkt í rásinni. Gerið graf af Φ(t), íspennunni og i(t) í rásinni. Hvaða tímaskalar koma við sögu og hvernig stýra þeir lausninni?
(Skilafrestur: Miðvikudagur 25. febrúar 2015 klukkan 17:00),
Lausnir skiladæma, gröf og skriftur
Tímadæmi: 7-29, 8-4, 8-8, og 8-16 í bók
- Flöt rafsegulbylgja í tómarúmi með bylgjulengd λ fellur lóðrétt á stóra velleiðandi plötu með þykkt d. Finnið τ(λ) og Γ(λ) fyrir kerfið. Gerið graf fyrir niðurstöðurnar. Gerum ráð fyrir að leiðarinn hafi enga segulverkun og segulsvörunarstuðullinn (permeability) sé μ0. Þetta gæti verið kopar eða ál, þó mikill munur sé á rafleiðni þeirra.
(Skilafrestur: Miðvikudagur 4. mars 2015 klukkan 17:00),
Lausn skiladæmis
Tímadæmi: 8-26, 10-2, 10-7, og 10-29 í bók
8. skammturinn er síðasti sameiginlegi skammturinn fyrir báða hópana.
- Hugsum okkur kjörþétti gerðan úr stórum samsíða hringlaga plötum.
Geisli platnanna er miklu stærri en geilin milli þeirra, a>>d. Í "Eðlisfræði
2" var reiknað hvers konar segulsvið myndast milli platnanna þegar þéttirinn er hlaðinn
eða þegar hann var tengdur við riðstraumgjafa. Þá var venjulega vitnað til tímaóháðu
lausnarinnar og gert ráð fyrir að E=E(t)az og segulsvið fékkst
í aφ stefnu. Hér eru notuð sívalningshnit með r mælt frá miðju þéttis,
z mælt hornrétt frá annarri plötunni að hinni og φ hornrétt á z og r.
Nú getum við séð að þetta er aðeins nálgun þó öllum jaðarhrifum sé sleppt.
Þéttirinn er tengdur við riðstraumgjafa, I(t)=I0cos(ωt). Skoðum jöfnur Maxwells án uppsprettuliða
fyrir fasora inni í þéttinum.
- Gerum ráð fyrir því að E=E(r,z)az og B=B(r,z)aφ. Finnið fjórar jöfnur fyrir E(r,z) og B(r,z) og sýnið að þær leyfa ekki lausnina úr "Eðlisfræði 2" nema í sértilfelli.
- Hvert er þetta sértilfelli og hvenær verður lausnin úr "Eðlisfræði 2" léleg nálgun?
- Finnið nálgunarlausnir fyrir E(r,z) og B(r,z) sem liðanir í tíðni eða bylgjuvigri upp í annars stigs leiðréttingu.
- Getum við fundið nákvæma lausn?
- Reynið grafíska framsetningu lausna.
Lausn skiladæmis
Tímadæmi: 11-02, 11-04, 11-07, og 11-15 í bók, ásamt eldri skiladæmum á vefsíðu námskeiðisins um geislun loftneta.
Prentvæn samantekt lausna fyrstu 8 dæmaskammta 2015
Viðar Guðmundsson
30.03.2015