Rannsóknir mínar
Ég stunda rannsóknir mínar á sviði þéttefnisfræði, nánar tiltekið
á rafeindum í hálfleiðurum. Hálfleiðarar eru notaðir í örgjörva og
minniseiningar í tölvur, fjarskiptatæki og hvaðeina annað.
Hálfleiðarar eru notaðir frekar en ofurleiðarar í þessi tæki
vegna þess að auðvelt er að stýra rafstraumi í gegnum þá með veikri
ytri rafspennu.
Þéttefnisfræðin lýsir öllu venjulegu og óvenjulegu efni í kringum
okkur. Innan hennar er fjallað um ofurleiðara, málma, lofttegundir,
vökva, ofurvökva, tauganet, einangrara, fjölliður, knattkol og
kristalla, það er flest þau kerfi sem sett eru saman úr fjölda
einda. Við erum ekki að greina efni niður í smæstu einingar
sínar, heldur að ráða þá gátu hvað gerist þegar mörgum eindum
er safnað saman. Upp úr þéttefnisfræðinni hafa því sprottið
aðferðir til þess að ráða við safn einda, fjöleindafræði og
safneðlisfræði.
Lotubundin rafeindakerfi
Kristalla er hægt að láta vaxa atómlag fyrir atómlag í sameindaúðurum.
Efnasamsetningu lagana má breyta til þess að rækta t. d. einangrandi
kristall ofan á hálfleiðandi kristall. Við samskeyti kristallanna
safnast frjálsar rafeindir saman í örþunnt lag. Rafeindirnar geta
aðeins ferðast samhliða skilfleti kristallanna en ekki þvert á hann.
Því er talað um tvívíð rafeindakerfi, rafeindirnar eru í raun þrívíðar
og rafkraftar þeirra berast í allar áttir en þær geta aðeins hreyft
sig í tveimur víddum.
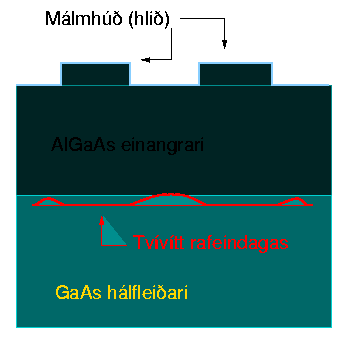
Hægt er að örmóta yfirborð einangrarans þannig að rafeindirnar
finni fyrir krafti sem er háður stöðu þeirra í tvívíðu sléttunni.
Til dæmis geta þær fundið fyrir lotubundnum krafti, þ. e. krafti
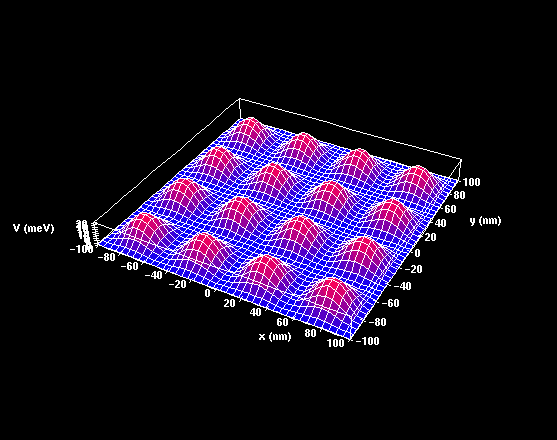
sem endurtekur sig reglulega. Ef við reynum að gera okkur mynd af þannig
krafti þá verðum við að ímynda okkur að rafeindirnar sjái hólalandslag
(andskammtapunktar)
eða pollalandslag (skammtapunktar)
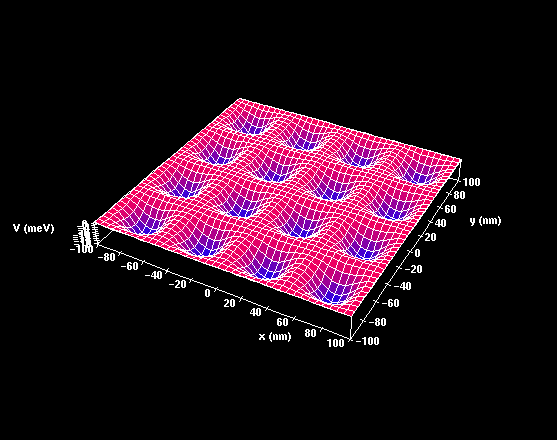
til þess að nefna tvö dæmi.
Ásamt samstarfsmönnum mínum, nemum í framhaldsnámi og erlendum
eðlisfræðingum, hef ég verið að reikna eiginleika slíkra rafeindakerfa.
Við beitum bæði handafli (blýanti og blaði) og tölvuafli til þess að kanna
eiginleika eins og ljósísog, seglun og leiðni.
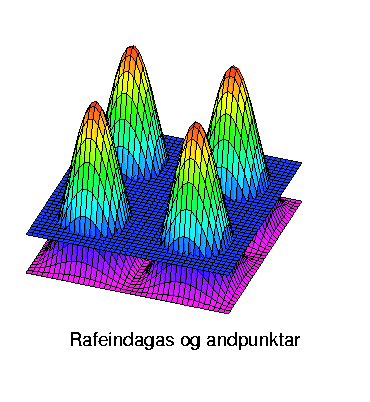
Venjulega eru líkön kerfanna
vel þekkt. Þau er hægt að setja fram sem stærðfræðilegar jöfnur.
Rafeindirnar í kerfinu víxlverka allar með rafkröftum vegna hleðslu þeirra.
Hreyfijöfnur einstakra rafeinda eru því allar tengdar á flókinn hátt.
Við vinnum með svokölluð miðsæ rafeindakerfi á mörkum smásærra
kerfa sem lýsa verður með skammtafræði og stórsærra kerfa sem hægt er að
lýsa með sígildri aflfræði. Miðsæjum kerfum verður því venjulega einnig
að lýsa með skammtafræði.
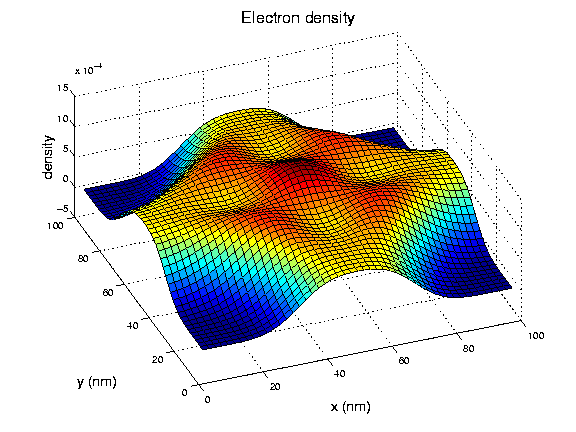
Vegna þess hve hreyfijöfnur einstakra rafeinda tengjast á flókinn hátt
er ekki hægt að giska á lausnir þeirra. Eignileikar kerfisins geta
gerbreyst þegar eindum er fjölgað, hitastigi breytt, eða ytra segulsviði
bætt við. Rafeindunum er stundum best lýst sem gasi, vökva eða jafnvel
kristalli, allt eftir því hvernig kennistærðum kerfisins er breytt.
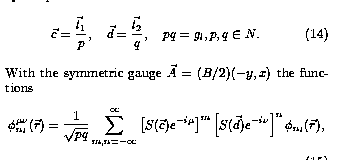
Venjulega er ekki hægt að leysa hreyfijöfnurnar nákvæmlega, ekki einu
sinni með tölulegum aðferðum í tölvu. Á þessari öld hafa verið þróaðar
margar nálgunaraðferðir og þeim lýst í grein sem kallast fjöleindafræði.
Mestur tími okkar eftir að líkan hefur verið valið fer í að beita
vissum nálgunum á hreyfijöfnurnar og skrifa forrit fyrir þær ef ekki er
hægt að leysa þær með handafli. Algengt er að þessi vinna taki frá
vikum upp í ár.
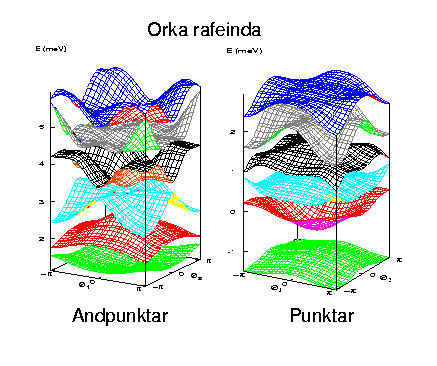
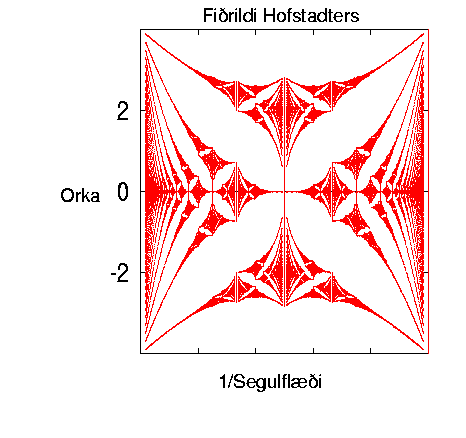
Hér að ofan eru orkuróf rafeinda í lotubundnu kerfi sýnd við eitt
visst gildi á segulsviði. Rafeind getur aðeins haft orkugildi sem
falla á vissa orkuborða (yfirborðin sem sjást á myndinni).
Myndin hér að neðan sýnir hvernig hvernig breidd þessara borða
breytist þegar segulstyrknum er breytt. Orkurófið fær
brotauppbyggingu (fractal). Vegna lögunar sinnar er það kallað
fiðrildi Hofstadters eftir þeim sem reiknaði það fyrst.
Þegar forrit er tilbúið er algengt að keyrsla þess fyrir eitt safn
kennistærða taki frá mínútum upp í mánuð á öflugri tölvu í hreinum
CPU-tíma (sá tími sem eitt verk út af fyrir sig fær í örgjörvanum).
Með öflugri tölvu á ég við tölvu sem gert getur meira en hundrað
milljón kommutöluaðgerðir á sekúndu. Síðan er keyrslan endurtekin
fyrir önnur söfn kennistærða eins oft og þarf og langlundargeð
allra viðkomandi leyfir.
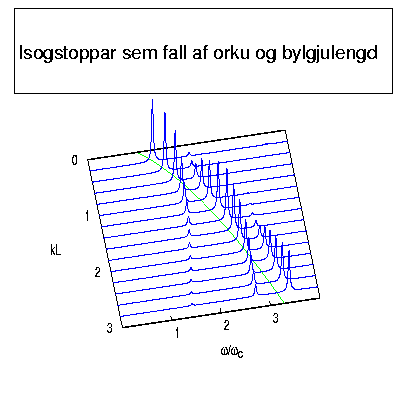
Einnig eru viðbrögð rafeindanna við ytra áreiti rannsökuð.
Hvað gerist þegar ljós fellur á kerfið og kemur rafeindunum
úr jafnvægi, eða rafspenna yfir kerfið reynir að koma þeim
á hreyfingu. Viðbrögðin eru hóphreyfingar þar sem aldrei
er hægt að örva stakar rafeindir, þær víxlverkast jú allar saman.
Fyrir vissar bylgjulengdir sleppur ljósið í gegnum kerfið án þess
að breyta nokkru fyrir rafeindirnar. Kerfið er þá gegnsætt.
En fyrir aðrar bylgjulengdir er hluti orku þess sogið upp og
notað í örvun hóphreyfinga. Bylgjur berast um kerfið eins og
gárur á polli.

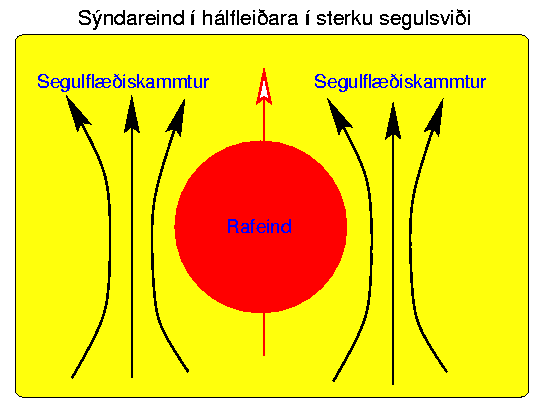
Algengt er að rafeindir í stóru safni týni einstaklingseðli sínu
og örvanir kerfisins eða ,,sýndareindir`` þess geti haft skrýtna
eiginleika. Í ofurleiðara geta sýndareindir verið rafeindapör,
í venjulegum málmi eru sýndareindir rafgasbylgjur, og í hálfleiðara
í segulsviði geta sýndareindirnar verið með brot af hleðslu
einnar rafeindar. Það þýðir þó ekki að einstakar rafeindir séu
samsettar úr smærri eindum.
Niðurstöðurnar verður að setja fram á grafískan hátt til þess að
bera saman við mæliniðurstöður tilraunahópa einhvers staðar í
veröldinni. Ef samræmi fæst milli niðurstaðna tilrauna og reikninga
eru niðurstöðurnar birtar sér eða með tilraunaniðurstöðum í
alþjóðlegum tímaritum um eðlisfræði þéttefnis. Niðurstöðurnar eru
þar öllum opnar. Sumt úr þessum grunnrannsóknum er notað af
hópum sem stunda tæknirannsóknir innan eða utan fyrirtækja
og sérhæfa sig í hagnýtingu fyrirbæra í þágu iðnaðar.
Ef niðurstöðunum ber ekki saman þá er okkur vissara að setjast niður
og athuga hvort líkanið eða nálgunin séu ekki í lagi. Eins er mögulegt
að forritið hafi verið gallað. Þetta gerist all oft og tekur mikinn
tíma að leysa úr. Í þessum ham erum við eins og
rannsóknarlögreglumenn sem ber að
gruna allt og alla og höfum ekkert annað að vopni en eðlisfræðina, reynsluna
og innsæið. Geti maður ekki fellt sig við þennan þátt vinnunar er vissara
að leggja eitthvað annað fyrir sig.
Nú er einmitt komið að kjarna málsins. Við erum að þessu vegna ánægju
okkar, forvitni og þeirra gullnu stunda þegar allt gengur upp og við
höfum skilið eitthvað sem enginn hafði botnað í áður.
Það er augljóst að líkanareikningar verða ekki gerðir í einangrun.
Við verðum að vera í góðu sambandi við tilraunahópa. Þetta samband
er vissulega gagnkvæmt því þeim gengur líka betur í samvinnu við okkur.
Þéttefnisfræðin er sú grein eðlisfræðinnar þar sem þessi tengsl eru
nánust. Tilraunir, líkanareikningar og tækni haldast afar þétt í hendur
innan greinarinnar. Það er einmitt þetta sem hefur orðið til þess að
hún hefur vaxið hraðar en nokkur önnur grein eðlisfræði á seinni
hluta 20. aldarinnar. Raftækniiðnaðurinn stendur nú á bak við
4-5% af heimsveltunni. Búist er við því að þetta hlutfall verði um
12-15% á næstu átta árum. Það tekst þó aðeins ef nægt framboð verður
á menntuðum einstaklingum, eðlisfræðingum, rafmagnsverkfræðingum,
tölvufræðingum og öðru tæknimenntuðu fólki. Skorturinn á hæfum
einstaklingum sést best á þeim launum sem hátæknifyrirtæki í
nágrannalöndunum bjóða upp á.

Styrktar og samstarfsaðilar
Rannsóknirnar hafa verið unnar á eðlisfræðistofu Raunvísindastofnunar
og styrktar af
- Rannsóknasjóði Háskólans
- Vísindasjóði Rannsóknarráðs
- Vísindasjóði NATO
- NorFA
Rannsóknirnar hafa verið unnar í samvinnu við
- Detlef Heitmann prófessor við Háskólann í Hamborg
- Rolf R. Gerhardts prófessor við Max-Planck Stofnunina í Stuttgart
- Daniela Pfannkuche sérfræðing við Max-Planck Stofnunina í Stuttgart
- Andrei Manolescu sérfræðing við Þéttefnisstofnunina í Búkarest
- Juan José Palacios sérfræðing við Háskólann í Madrid
- Arne Brataas fyrverandi Ph.D. nema við Tækniháskóla Noregs Þrándheimi
- Christop Steinebach doktorsnema við Háskólann í Hamborg
- Ingibjörgu Magnúsdóttur M.S. nema við Háskóla Íslands
- Sigurð I. Erlingsson M.S. nema við Háskóla Íslands
- Gunnar Pálsson fyrverandi B.S. nema við Háskóla Íslands
- Ágústu S. Loftsdóttur B.S. nema við Háskóla Íslands
auk fjölda frábærra tilraunamanna við hópa Heitmans við Háskólann
í Hamborg og von Klitzings við Max-Planck Stofnunina í Stuttgart.
Reikningarnir hafa verið gerðir á fjölda tölva um víða veröld,
tölvum Reiknistofnunar Háskóla Íslands, einkavélum ýmissa vísindamanna og
miðlægum tölvum rannsóknahópa.
Þri. 01.12 1998 10:47